Black Swan Events
Two Truths and a Take, Season 2 Episode 10

Hi everyone, a quick note from me: in a couple days, I’m going to send out a special email to all of you regarding COVID-19 and a few specific ways we can help out. Please read it - it’d mean a lot to me to see readers help out with a couple of local initiatives I’m looking to support.
So:
To be clear, I don’t think we can really call COVID-19 itself a Black Swan event. Plenty of people saw it coming, in some form or another, and said so. If you asked people last year, “what will trigger the next global event?”, some non-trivial number of people would probably say “a pandemic.” We were warned.
The resulting small businesses armageddon and unemployment tragedy might be, though. When we thought about pandemics, we typically forecasted either the immediate medical consequences, or went all the way to I am Legend scenarios where everyone is dead. But as far as I can tell, no one really foresaw: what happens when no one can leave their house for 3 months, so every small business closes all at once? (If you know of anyone who actually foresaw this ahead of time, please send it to me!)
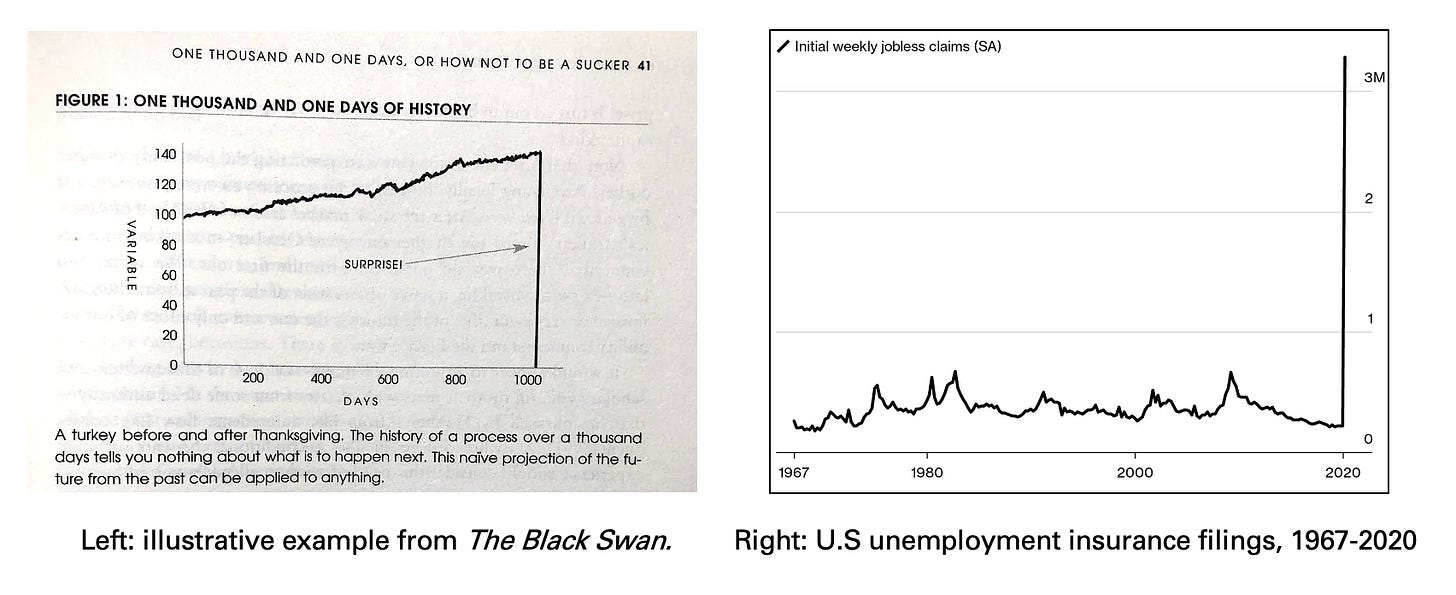
This is closer to real Black Swan stuff. This week’s unemployment filings, compared to the last half-century, are considered by frequentist statistics as a 30-sigma event: less likely to happen than if you had to select one atomic particle at random out of every particle in the universe, and then randomly again select that same particle five times in a row. A 30 sigma event should be outrageously unlikely, at universe-scale. But they happen. And when they do, they warn us: the problem is not that the universe didn’t behave correctly. The problem is that we were wrong.
This week, we’ll finish a makeshift trilogy of posts on Nassim Taleb’s books and their core concepts - following part 1 on Skin in the Game from last September, and part 2 on Antifragility over the past two weeks.
First, the basics. Black Swan Events have three principal characteristics:
One: They are unpredictable. This is the easiest one to grok, although the hardest to say anything actionable about. The term “Black Swan Event”, when used most lazily and colloquially, is simply meant to say “something we didn’t see coming.”
Two: Their magnitude. Unpredictable events aren’t rare; they happen every day. Black Swan Events aren’t just unpredictable in character; they’re also unprecedented in scale. The 2008 financial crisis caught everyone by surprise not because mortgage defaults or bad credit ratings were that unusual, but because the magnitude of the event broke through all expectations and safety valves. Something happens at a scale that no one considered possible before, and with consequences that no one has prepared for.
Three: They are retroactively explainable. In hindsight, we always see them coming. There were warning signs everywhere; the data pointed to such an event being within the realm of possibility; you know how it is. This retroactive explainability matters: there’s a logic to their retroactive explainability that is directly tied to their scale and their preemptive non-prediction.
If it were up to me, I would add a fourth essential characteristic, which is implied by the first three but I’d like to make explicit. Prior to the event, they are preemptively ruled out, either explicitly in our models or implicitly in our preparation for the future.
For an event to really be a Black Swan event, it has to play out in a domain that we thought we understood fluently, and thought we knew the edge cases and boundary conditions for possible realm. To me, this fourth characteristic is the real key for understanding the logic of Black Swan events, like what just happened this week.
Mediocristan vs. Extremistan
Let’s say you got together 1000 dentists, and then added up all of their annual income. Then you went out and found the most successful dentist on earth, and added his or her income to the total. How much will that super-dentist’s income change the mean average? Not much. Dentists earn a living day by day, patient by patient. Some dentists work faster and some dentists charge more, but it’s still a one-at-a-time kind of job.
If you were to plot the income of these dentists on a graph, you could plausibly expect them to look something like a normal distribution. It might not look like a true bell curve - it would likely have a longer tail towards richer dentists - but you don’t see any dentists making 100 million dollars a year.
If you used basic frequentist statistics to ask the question, “given our sample of 1000 dentists and their incomes, how likely is it that some dentist out there is earning 100 million dollars a year?”, you’d arrive at an impossibly low probability - 100 million is too many standard deviations, or “sigmas”, away from the mean. (When someone says that something is a “3 sigma event”, they mean an event whose magnitude lies three standard deviations away from the mean, which in a true Gaussian distribution, you’d expect to see maybe 1 in 1000 times.) Earning 100 million dollars a year for dental work would be, I dunno, a 7 sigma event or more? Something very unlikely, anyway.
Now instead of dentists, let’s take musicians. If you assemble 1000 random musicians, add up their annual income, and a then add Taylor Swift’s annual earnings to the total, the other 1000 people are going to be barely register as a rounding error. Musicians’ jobs scale in a way that dentists’ don’t.
Swift reportedly earned somewhere between 150 and 200 million dollars before taxes in 2019, and although that kind of experience is obviously atypical, it’s possible. We easily understand that musicians’ incomes do not follow a normal distribution, so asking “How many Sigma an event is Taylor Swift’s income” is pointless. Artists’ income doesn’t follow those rules. But we still think that dentists’ do. We have no reason to think otherwise, yet.

In The Black Swan, Taleb rhetorically uses two fictional places, “Mediocristan” and “Extremistan”, to illustrate the difference between these two environments. In Mediocristan, probabilities follow the laws of Normal Distributions, and calling something an “X sigma event” actually has meaning. In Extremistan, sigmas are meaningless. Tail events are understood and expected. (We’ve never seen one, but we intuitively understand that a 10+ magnitude earthquake will happen one day.)
Mediocristan and Extremistan are not fixed: the world is a changing place. Musical performance used to look like dentistry. You could only make a living performing live, in person - which does not scale all that well. But the invention of recorded music and the radio changed that. Music became scalable, and the distribution of musicians’ income turned into Extremistan. To a musician of the day, this was a “black swan” transformation of sorts: before recorded music, there was no conceivable way that you, or any musician, might entertain fifty million people a year. There was no way for musical performance to be so correlated. But now it’s routine.
When we talk about Black Swan Events and their principal characteristics (unpredictable; high magnitude; retroactively explainable; preemptively ruled out), what kind of events fit this description? High-magnitude events in domains that we thought belonged to Mediocristan (because we’d never seen evidence to the contrary), but actually belonged to Extremistan. This might be because that environment changed (new technology; new laws), but more likely, the environment was always that way. We were wrong, not the universe. We’d just never seen a tail event that big before, so we never considered that they were within the realm of possibility.
Don’t play Russian Roulette
Most people get this far ok. But then some people struggle with the next step: how might environments look like Mediocristan under some conditions, and give every impression of behaving by those rules, but then suddenly not? Where does our false confidence come from?
Our understanding of the world is based on past experience; the more events we’ve seen, the more confident we are in our model of how those events work. But when we gather these data points and draw conclusions from them, there’s a big difference - which often goes unnoticed - between gathering these data points in parallel (which can create an illusion of Mediocristan), versus gathering them in repeated doses (which reveals the Extremistan that was there all along.)
Let’s do a thought experiment. Imagine a group of twenty friends heads to the casino, each equipped with $100, and they head to the roulette table. They each play for an hour. At the end of the hour, some people are up, some people are down, a few have gone bankrupt. Overall, if you asked scientifically, “what is the effect of Roulette on your wallet?”, you might draw up a probability distribution and conclude, "OK, the expected value of playing roulette is less than breakeven, but it’s a distribution, and it looks like this."
Now let’s imagine a new scenario. Instead of twenty friends playing for one hour, it’s just one person, playing for twenty hours. Are you going to draw the same conclusion about the effects of Roulette on wallets? No. That one person is overwhelmingly likely to have gone bankrupt, if they’re compelled to keep playing over and over again.

There is a clear difference between what roulette does to a group of people in parallel, versus what roulette does to one person in repeated doses. (If you’re not convinced, make the game more extreme: you’re offered a chance to play Russian Roulette for a million dollars cash. What is the expected value of playing? What about playing six times?)
What is different? The wheel is the same; the odds are the same. But there is a difference. Every time you spin the wheel, on average there will be a slightly negative expected outcome; but when that negative outcome can be separated and born separately by 20 different friends, each with their own wallet, the odds of any one of them going bankrupt are smaller.
But when that the outcomes are all concentrated on one wallet, that one wallet will go bankrupt before not too long. Bankruptcy is a tripwire, where the consequences change in character. When you go bust, you can no longer buy back in, and your luck is no longer eligible to “average back out” to the mean expected outcome that 20 friends saw over their one hour of playing.
The point of this is, if you watch people play roulette for 30 years, but the only data points you’re observing are people playing in one-hour increments, then it’s true that you’ve learned something - your model of “what is the effect of one hour of roulette on your wallet” is probably pretty refined. But that does not mean you understand roulette generally. And it does not mean that you’re prepared to play roulette for 20 straight hours.
The Problem of Induction
The central example in The Black Swan is a rephrased parable called the Turkey Problem:
Consider a turkey that is fed every day. Every single feeding will firm up the bird’s belief that it is the general rule of life to be fed every day by friendly members of the human race “looking out for its best interests”, as a politician would say. On the afternoon of the Wednesday before Thanksgiving, something unexpected will happen to the turkey. It will incur a reversion of belief.
The future hasn’t happened yet. More things can happen than will; and more things will happen than have happened. The future holds infinite possibility, while the past only offers a finite set of examples to learn from.
Our Roulette Scientist who has only ever seen people play roulette for an hour at a time knows something about roulette, but not everything. He may have watched thousands of individual hours of roulette on a cumulative basis, but that doesn’t prepare him for 20 hours consecutively. They are not the same thing. If tomorrow he is suddenly compelled to play for 20 straight hours, his understanding of the game, as Taleb would put it, will incur a reversion of belief.
When the dust settles and our Roulette Scientist looks back on what happened, and how he could have been so wrong in his understanding of roulette, he’ll offer himself a retroactive explanation: “all at once” is different from “one at a time”, he’ll sigh. That’s really obvious in hindsight, and it doesn’t require that much of an adjustment to his understanding of roulette. But that tiny little adjustment makes all the difference. If “all at once” isn’t something you’ve ever thought about, then of course it’s not part of your threat model.
Connecting parts one and two together here: we’re most at risk for getting turkeyed when we’ve studied some corner of the world, and have a lot of data telling us: here’s how this system behaves. Here are its parameters. Here are its upper and lower bounds. It behaves like something out of Mediocristan. There are years and years of data reaffirming this is true.
Up until last week, the chart of US weekly unemployment claims sure looked a whole lot like Mediocristan. Job losses are something that happen more or less in parallel: in a dynamic free market economy, Alice losing her job in Seattle is not that correlated with Bob losing his job in Tampa.
There are some correlations with economic cycles, for sure; no one believed that jobless claims were completely independent of one another. But we had decades of data showing us, here’s what "Shutdown” looks like during good years and bad, during national crises like 9/11 and economic crises like 2008. We even have data showing us what happens when “Shutdown” scales up to an entire city for two months, like with hurricane Katrina.

We didn’t really consider: but what if every business closes for two months, all at once, because no one is allowed to leave their house anymore? In hindsight, yeah that’s pretty much what you’d expect would happen in a pandemic. But no one had ever seen “Shutdown” scale up to that level before. It was not in the model.
Our years and years of looking at jobless claims - which, in total, constitute far more total claims than this week’s 3 million - are not really useful here. That was all learning in parallel. Now we’re dealing with a repeated dose situation, and a degree of sudden, concentrated unemployment at a scale where we do not have any prior experience. The human cost will be so, so big.
Part of that cost, tragically, is that we’re in no way ready to handle that much unemployment, so suddenly. The American health care system is tied to employment, and at a moment where we’re all about to get sick and risk death, everyone is getting laid off and losing their health insurance. The system we have in place for processing jobless claims, and supporting small businesses in lean times, is just not ready for a sudden event of this magnitude. And why would it? We had fifty years of experience, stress testing what normal looks like and what high looks like.
Then 2020 happened. And we were all wrong.
As an additional reminder - please remember to check your inbox in a couple days for a special COVID-19 related issue.
And finally, this week’s comic section, the tweet that made me laugh the hardest: